2.9.1 Transforms

A transform specifies a rule that takes an expression from one form to another. It is introduced by the special symbol ʈ followed by pattern, replacement and optional constraint expressions. If the pattern matches a selected expression and the constraints are met, the pattern is transformed using wildcard replacement. The constraints specify parts of the pattern that must meet certain criteria. Collectively, the constraints form a Boolean expression. 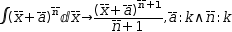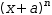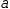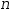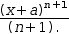For example, ʈ∫(x+a)^n ⅆx→(x+a)^(n+1)÷(n+1), a:k∧n:k is a transform that takes an integral of the form (x+a)^n, where a and n are any real values, to the form (x+a)^(n+1)÷(n+1).

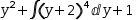
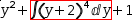
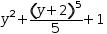
To apply a transform, add a transform like the one above to the workspace. Then add another expression to be worked on, like y^2+∫(y+2)^4 ⅆy+1. Select the part of the expression to be transformed (e.g., y^2+.{∫(y+2)^4 ⅆy}+1)) and apply Expressions Transform . The expression will be transformed to y^2+(y+2)^5÷5+1.

Transforms can participate in property lists (§2.9.3) and rule sets (§8.1.7). They make use of substitution rules (§8.1.7) and pattern matching (§9.1.1). The transform action is described more fully in §3.3.5